m x n 크기의 Grid 와 하나의 Ball 이 Grid 의 [startRow, startCol] 위치에 주어졌을 때, 이 Ball 이 Grid 밖으로 나가게 되는 경우의 수를 구하는 문제. 문제에서 Ball 은 한 번에 가로 / 세로 방향으로만 움직일 수 있고, 최대 움직임 횟수는 제한된다.
처음 문제를 확인하고 Brute Force 방식으로 해결하면 될 것 같다는 생각을 하고 풀이를 시작했는데, 공이 한 번 위치한 장소에 다시 돌아올 수 있기 때문에 완전 탐색 방식은 시간이 너무 오래 걸렸다. 그래서 변경한 풀이 방식은, m x n 행렬에 움직임의 횟수 별로 공이 각 칸에 위치할 수 있는 경우의 수를 저장하고 이를 통해 Grid 밖으로 나갈 수 있는 경우의 수를 구하는 방식이다.
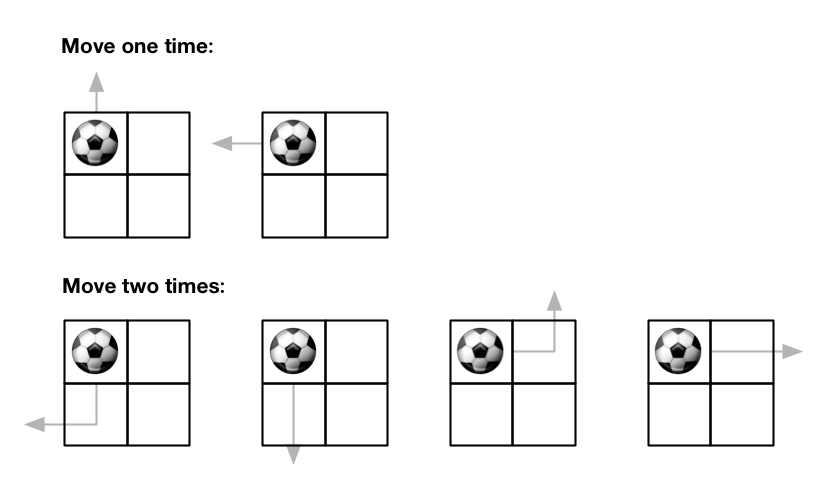
위의 그림을 통해 설명하면, 공의 초기 위치가 (0, 0) 이므로 초기 행렬은 아래와 같이 표현이 가능하다. 이 때, 공이 Grid 밖으로 나갈 수 있는 경우의 수는 (0, 0) 에서 위 방향 / 왼쪽 방향 총 두 경우이다.
| 1 | 0 |
| 0 | 0 |
공이 한 번 움직이고 난 다음의 행렬은 아래와 같다. 이 때, 공이 Grid 밖으로 나가는 경우는 (0, 1) 위치에서 위 / 오른쪽 방향, (1, 0) 위치에서 왼쪽 / 아래 방향, 총 네 가지이다.
| 0 | 1 |
| 1 | 0 |
위 그림에서, 공이 움직일 수 있는 최대 횟수는 2번으로 제한되어 있으므로 두 번 움직이고 난 후의 경우는 구할 필요가 없다. 한 번 움직여서 Grid 를 벗어나는 경우가 2가지, 두 번 움직여서 Grid 를 벗어나는 경우가 4가지 이므로 총 6개가 답이 된다.
이와 같은 풀이로 작성한 코드는 다음과 같다.
const int MOD = (int)1e9 + 7;
int dr[4] = {-1, 0, 1, 0}, dc[4] = {0, -1, 0, 1};
int dp[51][51], tmp[51][51];
class Solution {
public:
int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
dp[i][j] = tmp[i][j] = 0;
dp[startRow][startColumn] = 1;
int ans = 0;
for (int move = 1; move <= maxMove; move++) {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0) ans = (ans + dp[i][j]) % MOD;
if (j == 0) ans = (ans + dp[i][j]) % MOD;
if (i == m - 1) ans = (ans + dp[i][j]) % MOD;
if (j == n - 1) ans = (ans + dp[i][j]) % MOD;
tmp[i][j] = 0;
if (i > 0)
tmp[i][j] = (tmp[i][j] + dp[i - 1][j]) % MOD;
if (j > 0)
tmp[i][j] = (tmp[i][j] + dp[i][j - 1]) % MOD;
if (i < m - 1)
tmp[i][j] = (tmp[i][j] + dp[i + 1][j]) % MOD;
if (j < n - 1)
tmp[i][j] = (tmp[i][j] + dp[i][j + 1]) % MOD;
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = tmp[i][j];
}
}
}
return ans;
}
};'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode # 135] Candy (0) | 2021.06.27 |
|---|---|
| [LeetCode # 315] Count of Smaller Numbers After Self (0) | 2021.06.26 |
| [LeetCode # 52] N-Queens II (0) | 2021.06.18 |
| [LeetCode # 51] N-Queens (0) | 2021.06.18 |
| [LeetCode # 44] Wildcard Matching (0) | 2021.06.17 |
