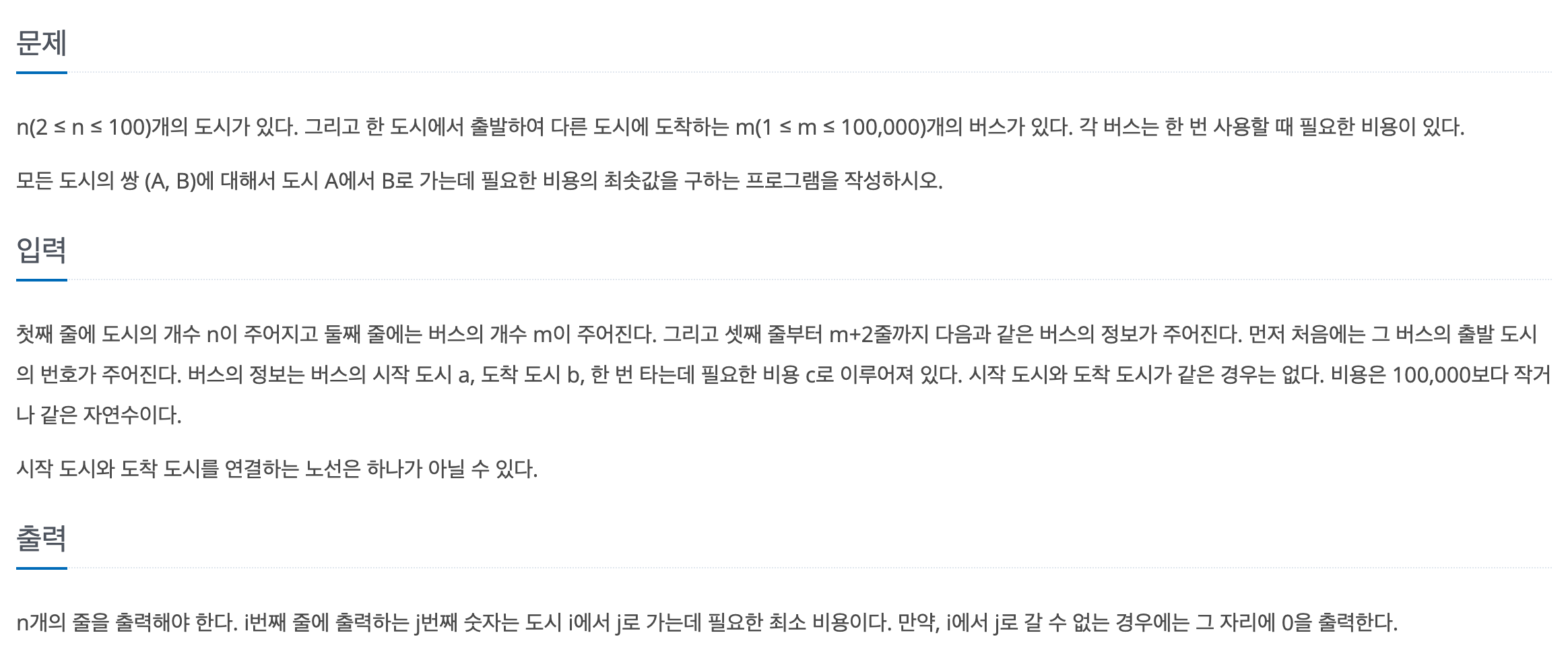
주어진 문제는 위와 같다. 최대 100 개의 도시가 주어지고, 도시 간 이동이 가능한 버스 노선들이 주어졌을 때 모든 도시 간 이동 시의 최소 비용을 구하는 것이다. 최단 경로 탐색을 위한 알고리즘은 다익스트라, 벨만 포드, A* 탐색 등 여러 가지가 있지만 위와 같이 모든 노드 간 최단 경로를 구하기 위한 알고리즘으로 문제의 이름과 같은 플로이드 와샬 알고리즘이 있다.
플로이드 와샬 알고리즘에 대해 내가 기억하고 있는 것은, 노드 간 경로 가중치를 테이블에 저장하고 경로가 존재하지 않는 경우는 INF 값으로 저장한다. 그 뒤 스텝 별로 중간에 다른 노드를 경유하며 경로 가중치를 업데이트하는 방식으로 기억하고 있었다. 하지만 내가 기억하고 있는 알고리즘의 로직은 너무 모호해 문제 풀이에 적용할 수 없었고 따로 플로이드 와샬 알고리즘을 찾아본 뒤 문제를 해결했다.
플로이드 와샬 알고리즘
플로이드 와샬 알고리즘을 간단하게 설명하면, O(|V|^3) 의 시간 복잡도를 갖는 모든 쌍 최단 경로 탐색 알고리즘이다. 매 스텝 별로 X to Y (X, Y 는 노드) 경로의 가중치를 업데이트 해야 하므로 O(|V| ^ 2) 를 매 스텝 별로 실행하고, 각 스텝은 경유할 노드를 순차적으로 적용하므로 O(|V| ^ 2 * |V|) 의 시간 복잡도를 갖게 된다.
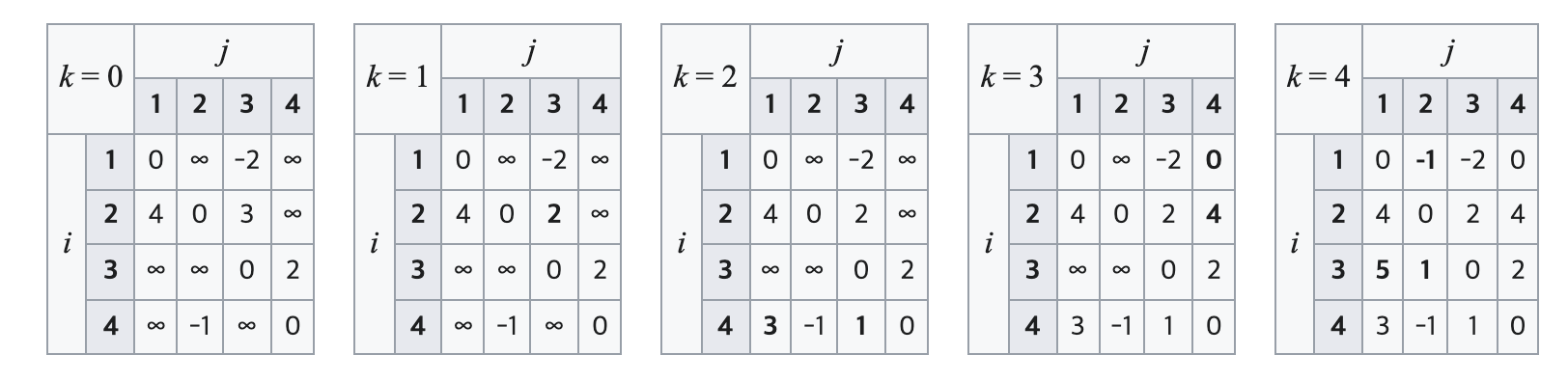
k = 0 일 때, 해당 테이블은 노드를 경유하지 않고 i - j 간 경로를 표현한 것이다.
k = 1 일 때, 변경된 table[2][3] 값은, 기존의 node(2) -> node(3) 의 경로 가중치는 3이고, 노드 1번을 경유한 node(2) -> node(1) -> node(3) 의 가중치 합이 4 + (-2) 이므로 새로운 값이 업데이트된 것을 볼 수 있다.
k = 2 일 때, node(4) -> node(1) 의 경로와 node(4) -> node(3) 의 경로가 2번 노드를 경유함으로 인해 가중치 값이 업데이트된 것을 확인할 수 있다.
이와 같이 경유할 노드를 변경해 가며 경로 가중치 값을 업데이트해 나가면 최종적으로 모든 노드 쌍 간의 최단 경로를 구할 수 있게 된다.
알고리즘을 적용한 코드는 3개의 for 문을 중첩함으로써 간단하게 구현이 가능하고, 이를 적용해 문제 해결에 사용한 코드는 다음과 같다.
#include <iostream>
using namespace std;
const int CITY = 100;
const int INF = 123456789;
int city, bus;
int dist[CITY + 1][CITY + 1];
void initialize() {
for (int i = 1; i <= city; i++) {
for (int j = 1; j <= city; j++) {
dist[i][j] = INF;
}
}
}
void input() {
cin >> city >> bus;
initialize();
for (int i = 0; i < bus; i++) {
int a, b, c;
cin >> a >> b >> c;
dist[a][b] = dist[a][b] < c ? dist[a][b] : c;
}
}
void output() {
for (int i = 1; i <= city; i++) {
for (int j = 1; j <= city; j++) {
if (dist[i][j] == INF) {
cout << "0 ";
} else {
cout << dist[i][j] << " ";
}
}
cout << "\n";
}
}
void solve() {
for (int k = 1; k <= city; k++) {
for (int i = 1; i <= city; i++) {
for (int j = 1; j <= city; j++) {
if (i == j)
continue;
int k_dist = dist[i][k] + dist[k][j];
dist[i][j] = dist[i][j] < k_dist ? dist[i][j] : k_dist;
}
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
input();
solve();
output();
}
# Reference.
플로이드-워셜 알고리즘 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서, 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 변의 가중치가 음이거나 양인 (음수 사이클은 없는) 가중 그래프에서 최단 경로들을 찾는 알고리즘이다.[1][2] 알고리즘을 한 번
ko.wikipedia.org
'Algorithm > Baekjoon' 카테고리의 다른 글
| [BOJ # 1874] 스택 수열 (0) | 2021.09.21 |
|---|---|
| [BOJ # 1600] 말이 되고픈 원숭이 (0) | 2021.09.19 |
| <BOJ 2508> 나무 자르기 (0) | 2019.02.14 |