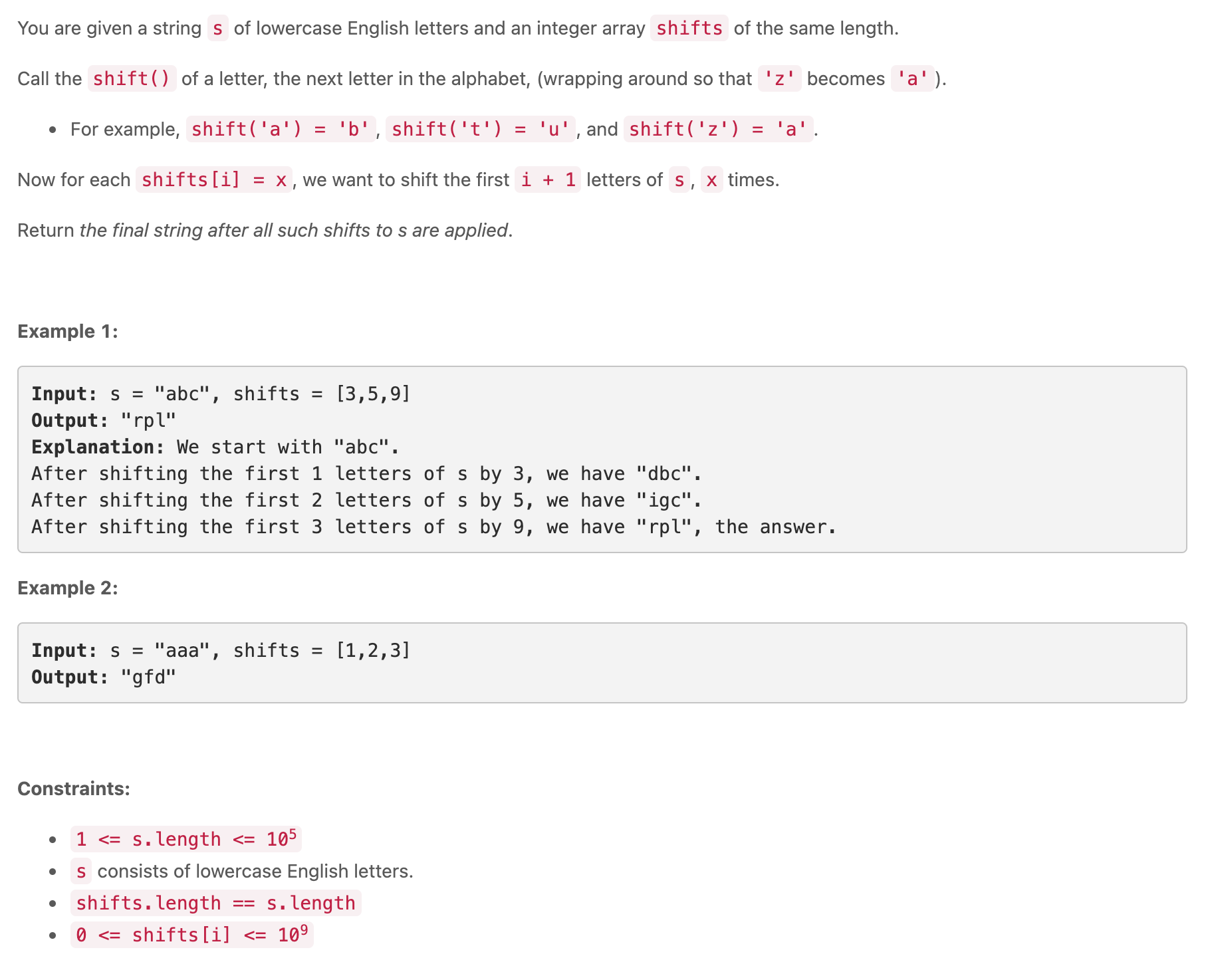
주어진 문제는 위와 같다. 두 개의 문자열 's1', 's2' 가 주어졌을 때, s1 을 scramble 해서 s2 으로 만들 수 있는 지를 확인하는 문제이다. 문자열을 scramble 한다는 것은 위에서 다음과 같이 표현한다.
- 문자열의 길이가 1이라면 멈춘다.
- 문자열의 길이가 1보다 큰다면, 다음을 따른다.
- 문자열의 임의 인덱스를 정해서 해당 인덱스를 기준으로 두 개의 문자열로 나눈다. (두 개의 문자열은 빈 문자열이 될 수 없다.)
- 나눠진 두 개의 문자열을 임의 순서로 배치한다.
- 나눠진 문자열에 대해 1. 부터 다시 수행한다.
이 문제를 해결하기 위해, 재귀함수를 사용할 수 있었다. 두 문자열을 임의의 인덱스 (모든 인덱스에 대해) 기준으로 각각 두 개의 문자열로 쪼갠다. 그리고 쪼개진 문자열의 순서를 바꿔가며 비교한다.
예를 들어, s1 이 "ab", s2 가 "ba" 라고 주어졌다면 각각의 문자열을 두 개로 나눈다. (문자열의 순서를 바꾸며 비교하는 것을 표현하기 위해 극단적으로 길이가 2인 문자열로 예시를 만들었다.) s1 을 두 개의 문자열로 나누면 "a", "b" 가 되고, s2 를 두 개의 문자열로 나누면 "b", "a" 가 된다. 순서를 유지한 채로 비교를 하면 "a" == "b" / "b" == "a" 가 되고, 순서를 바꾸면 "b" == "b" / "a" == "a" 가 된다. 순서를 바꿔 비교했을 때 두 문자열이 같음을 확인할 수 있으므로 s1 과 s2 는 문제의 조건을 만족한다.
이와 같이, 각각의 문자열이 주어졌을 때 문자열을 나눠서 다시 그것을 판정하는 방식으로 재귀함수를 작성하면 문제를 해결할 수 있을 것으로 생각했다. 이를 적용한 소스 코드는 다음과 같다.
class Solution {
public:
bool isScramble(string s1, string s2) {
if(s1==s2)
return true;
int len = s1.length();
int count[26] = {0};
for(int i=0; i<len; i++)
{
count[s1[i]-'a']++;
count[s2[i]-'a']--;
}
for(int i=0; i<26; i++)
{
if(count[i]!=0)
return false;
}
for(int i=1; i<=len-1; i++)
{
if( isScramble(s1.substr(0,i), s2.substr(0,i)) && isScramble(s1.substr(i), s2.substr(i)))
return true;
if( isScramble(s1.substr(0,i), s2.substr(len-i)) && isScramble(s1.substr(i), s2.substr(0,len-i)))
return true;
}
return false;
}
};이와 같이 작성한 소스코드는 문제를 정확히 풀이하는 데는 문제가 없었지만, 제출 시 TLE 가 발생했다. 재귀함수의 형태를 취했는데 알파벳의 개수를 비교한 것 외에 가지치기가 전혀 이루어지지 않은 점이 문제로 생각됐다. 추가적인 가지치기가 가능한 방법은, 이미 지나갔던 경로를 재탐색하지 않도록 하는 것이라 생각했다.
예를 들어, isScramble("abcde", "caebd") 은 false 를 반환한다. 만약 주어진 문제에서 부분문자열을 나누다가 이와 같은 형태를 마주쳤을 때 굳이 이 문자열을 나눠가며 판정하지 않고 바로 false 를 반환할 수 있다면 문제의 해결에 시간이 단축될 것이다. 하지만 이러한 값을 일일히 넣어줄 수 없으니 주어진 문자열을 가지고 로직을 수행하다 마주치는 경우에 대해 가지치기를 할 필요가 있어 보였다.
이를 위해 해시맵을 추가적으로 적용했으며, s1 의 문자열과 s2 의 문자열을 붙여 해시맵의 키로 활용했다. 이를 적용한 소스 코드는 다음과 같다.
class Solution {
public:
map<string, bool> hash;
bool isScramble(string s1, string s2) {
if (s1 == s2) {
return true;
}
if (hash.find(s1 + s2) != hash.end()) {
return hash[s1 + s2];
}
int len = s1.length();
int cnt[26] = {0,};
for (int i = 0; i < len; i++) {
cnt[s1[i] - 'a']++;
cnt[s2[i] - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (cnt[i] != 0) {
hash[s1 + s2] = false;
return false;
}
}
bool res = false;
for (int i = 1; i < len; i++) {
res = res || isScramble(s1.substr(0, i), s2.substr(0, i)) && isScramble(s1.substr(i), s2.substr(i));
res = res || isScramble(s1.substr(0, i), s2.substr(len - i)) && isScramble(s1.substr(i), s2.substr(0, len - i));
}
hash[s1 + s2] = res;
return res;
}
};위의 코드에서 볼 수 있듯이, 기존의 코드에서 변경된 부분은 해시맵이 적용된 부분이다. 가지치기를 위해 함수 호출 시 해시맵에서 이미 존재하는 경우인 지를 확인하고 이미 해시맵에 저장이 된 경우 저장된 값을 반환한다. 또한 현재 문자열 s1, s2 를 가지고 판정한 결과값을 해시맵에 저장함으로써 추후 가지치기에서 활용할 수 있도록 한다.
해시맵을 적용해 일종의 DP 방식을 활용한 결과 TLE 를 피하고 문제를 풀이할 수 있었다.
'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode # 446] Arithmetic Slices II - Subsequence (0) | 2021.09.10 |
|---|---|
| [LeetCode # 848] Shifting Letters (0) | 2021.09.09 |
| [LeetCode # 84] Largest Rectangle in Histogram (0) | 2021.09.08 |
| [LeetCode # 206] Reverse Linked List (0) | 2021.09.08 |
| [LeetCode # 68] Text Justification (0) | 2021.09.07 |