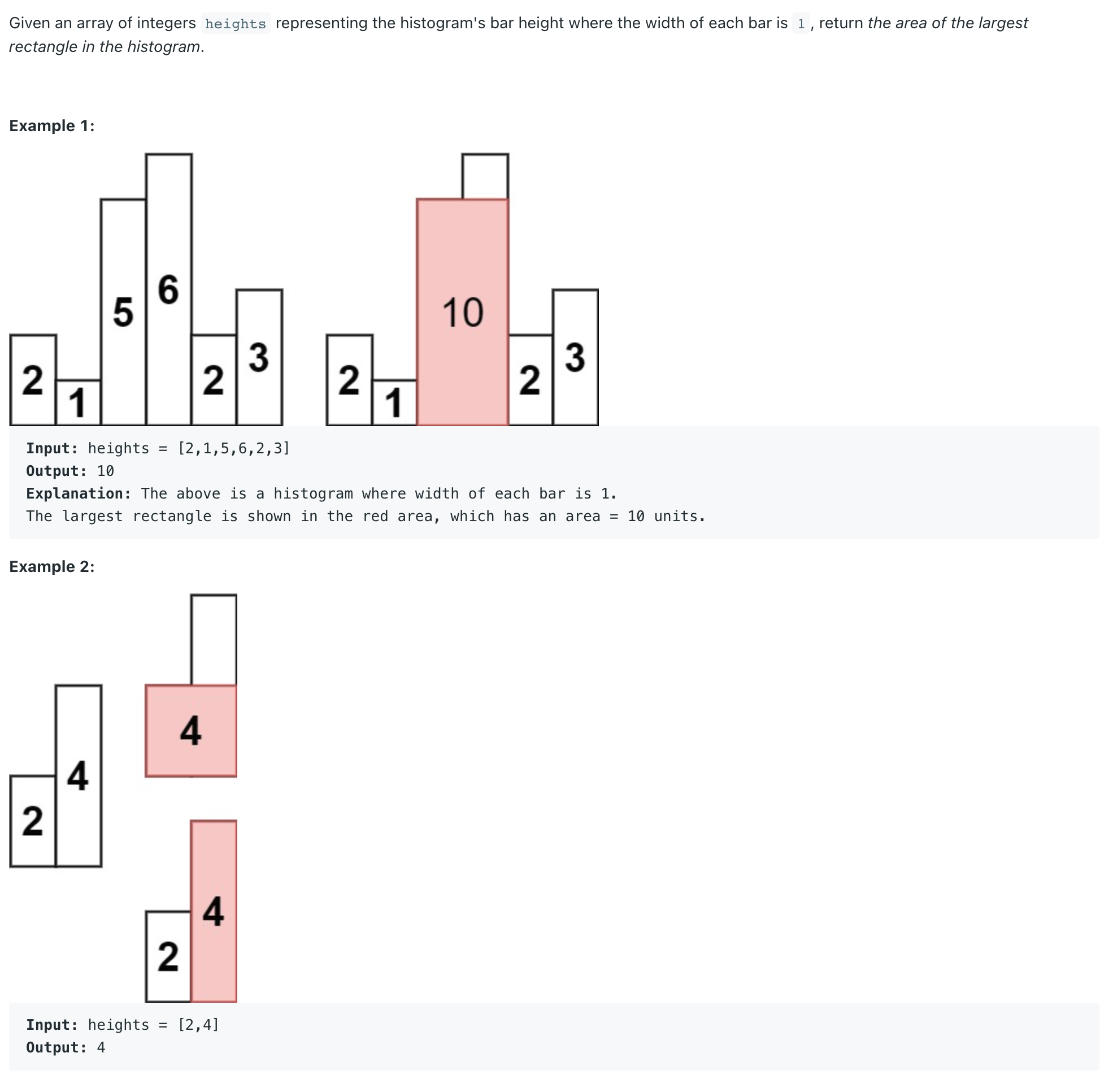
주어진 문제는 위와 같이 히스토그램에서 가장 큰 넓이를 갖는 직사각형을 찾는 것이다.
가장 간단한 해결 방법은, 각 위치 별로 좌우로 확장시키며 가질 수 있는 최대 넓이를 확인하는 것인데 이러한 방법은 O(n^2) 의 시간복잡도를 갖는 해결 방법이기 때문에 사용할 수 없었다.
대신 문제의 해결을 위해 스택을 사용하는 방식을 적용할 수 있었다. 왼쪽부터 오른쪽으로 탐색하며 히스토그램 블록의 높이가 점차 증가하도록 스택을 관리한다. 히스토그램 블록의 높이가 지속적으로 증가한다면 계속해서 스택에 해당 위치를 저장하고, 높이가 감소할 경우 현재 스택에 저장된 최대 높이를 갖는 블록에 대해 넓이를 계산한다.
위의 <예제 1> 을 통해 설명을 보강하자면, 처음 스택은 빈 상태로 시작을 하고 첫 번째 인덱스를 저장하게 된다.
스택 : {0}, 최대 넓이 : 0
인덱스가 1일 때, 히스토그램의 높이는 스택에 저장된 인덱스 블록보다 낮으므로 현재까지의 넓이를 계산해 저장한다. 그 뒤 스택이 비어있으므로 인덱스를 다시 스택에 저장한다.
스택 : {}, 최대 넓이 : 2
그 뒤로는, 블록의 높이가 점차 높아지므로 계속해 스택에 인덱스를 저장한다.
스택 : {1, 2, 3}, 최대 넓이 : 2
인덱스가 4가 됐을 때, 다시 블록의 높이가 낮아지므로 높이를 계산한다. 이 때, 현재 탐색 중인 인덱스는 4이고 스택의 탑에 저장된 인덱스는 3, 그 다음 탑의 인덱스는 2이므로 인덱스 3의 높이를 가지고 계산할 수 있는 넓이는 하나의 블록 넓이 뿐이다.
스택 : {1, 2}, 최대 넓이 : 6
다시 인덱스 4에서, 블록의 높이가 아직 낮으므로 높이를 다시 계산한다. 현재 탐색중인 인덱스는 4, 스택의 탑에 저장된 인덱스는 2, 그 다음 인덱스는 1이므로 인덱스 2의 높이를 가지고 계산할 수 있는 넓이는 인덱스 2와 3의 블록 넓이이다. 따라서 넓이는 5 * 2 = 10 이 된다.
스택 : {1}, 최대 넓이 : 10
이러한 방식으로, 스택에 계속해 인덱스를 저장하고 높이를 계산하는 것을 반복하며 최대 넓이를 계산할 수 있다. 이러한 풀이 방식은, 인덱스를 0 에서 n - 1 까지 순차 탐색하며 저장 / 계산 최대 2번 연산을 수행하므로 O(2n) 의 시간 복잡도 (O(2n) 은 O(n) 으로 표현 가능하다) 를 갖는다고 볼 수 있다.
이러한 풀이 방식으로 작성한 소스 코드는 다음과 같다.
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> s;
int maxArea = 0;
for (int i = 0; i <= heights.size(); i++) {
int h = i == heights.size() ? 0 : heights[i];
if (s.empty() || h >= heights[s.top()]) {
s.push(i);
}
else {
int top = s.top();
s.pop();
int area = heights[top] * (s.empty() ? i : i - 1 - s.top());
maxArea = maxArea > area ? maxArea : area;
i--;
}
}
return maxArea;
}
};'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode # 446] Arithmetic Slices II - Subsequence (0) | 2021.09.10 |
|---|---|
| [LeetCode # 848] Shifting Letters (0) | 2021.09.09 |
| [LeetCode # 206] Reverse Linked List (0) | 2021.09.08 |
| [LeetCode # 68] Text Justification (0) | 2021.09.07 |
| [LeetCode # 1629] Slowest Keys (0) | 2021.09.07 |
